StoTree implements a form of the Markovian utility function. Let y^th denote a duration t visit to state y followed by any other sequence h of states and durations. If x is the previously visited state, then the Markovian utility assigned to y^th is equal to

Here w(y|x) is a toll associated with the transition from x to y; v(y) is a quality rate specific to state y, and a(y) is a discount factor. At a stochastic fork

in which subtrees K_i are reached from state y at competing rates l_i, the rollback equation for calculating expected utility can be shown to take the simple form

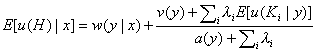At a chance fork with associated probabilities p_i, the usual probability-weighted average is used:

StoTree repeatedly evaluates these equations for the user-specified multi-factor stochastic tree. In this context, the states y are vectors y = (y₁, …, y_m), where y_i is the state of the i^th factor.